Compensating for roll when controlling rudder

2023-09-10

The problem

When we’ve been out testing the Eel in the water, we’ve realised that the thrust motor has made the Eel roll occasionally. The problem arises when we turn the rudder. Let’s say we turn the rudder to the right and the Eel has a roll like in the diagram below, then the rudder would in reality be pointing downwards, which would make the Eel dive. The rudder is in reality moving both horizontally AND vertically, while we just want to move it horizontally. That’s a problem.

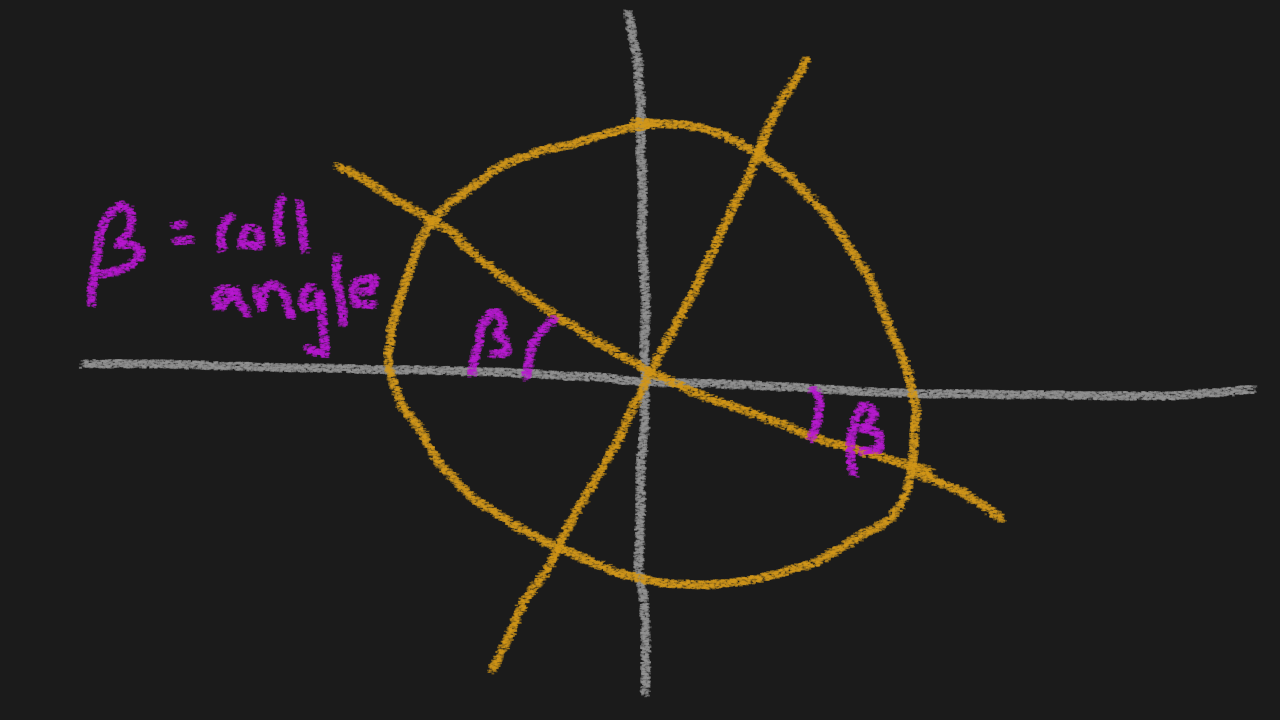
The solution

The beauty of this is that we had all the tools to solve this. Recently Gunnar rebuilt the rudder, from a regular plate rudder to making the propeller itself adjustable. As a bonus, he also made it controllable not only horizontally, but also vertically. You can see it in action in the video below.

This meant that we are in control of adjusting the Eel’s turn axis to the extent that we in theory can compensate for potential roll.

The other part to the solution was that we already had the roll angle as an output from the BNO055 IMU sensor, which also has been very stable and reliable so far.

With these inputs and outputs, we could now solve the problem of possible roll angles when turning. We just had to remember the math from school…

After some thinking, we realised that the rotation matrix is for exactly these kinds of applications. Let’s look at the diagram below:

If we turn the propeller (or rudder, it doesn’t really matter what it is) in an arbitrary vector, like the orange one in the image, then it’s actually quite simple to compensate for the roll angle by just rotating the vector backwards. So in this case: the negative value of the roll angle.

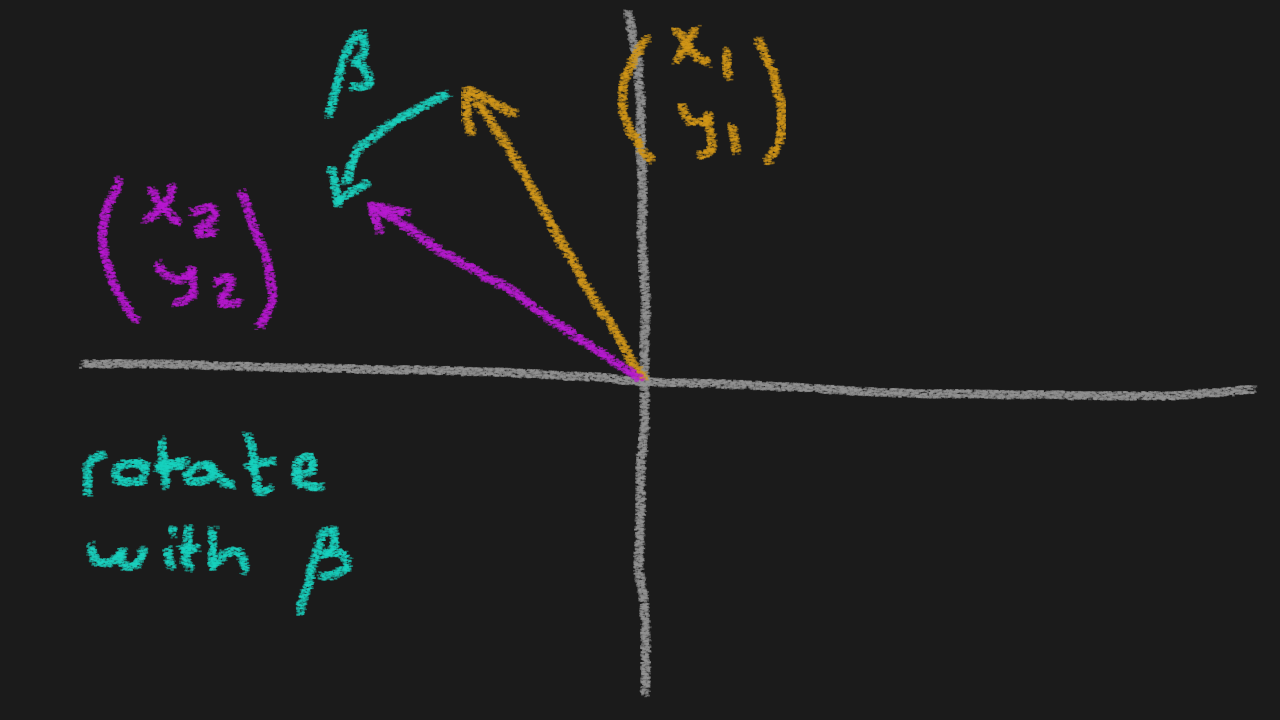
The rotation matrix looks like this:

$\begin{bmatrix}x_2\\y_2\end{bmatrix} = \begin{bmatrix}x_1cos β - y_1sin β\\x_1sin β + y_1cos β\end{bmatrix}$

where $\begin{bmatrix}x_2\\y_2\end{bmatrix}$ is the new vector after rotation,

where $\begin{bmatrix}x_1\\y_1\end{bmatrix}$ is the original vector

and $β$ is the angle of rotation.

You can see the roll angle compensation in the video below. It’s perhaps not too easy to see, but in this case we’ve set the propeller to point upwards. As we roll the Eel, the propeller auto-corrects itself so that the propeller points upwards, despite any roll.